ОБЩИЕ ПРОБЛЕМЫ В УЧЕТЕ ВАРИАЦИЙ ПРИХОДЯЩЕЙ СОЛНЕЧНОЙ РАДИАЦИИ В ФИЗИКО-МАТЕМАТИЧЕСКИХ МОДЕЛЯХ КЛИМАТА

В.М. Федоров

Московский государственный университет имени М.В. Ломоносова

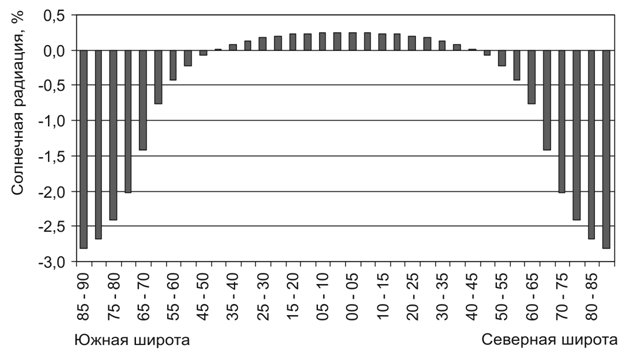
1.Входной энергетический сигнал. В настоящее время в качестве входящего в климатическую систему Земли внешнего энергетического сигнала в радиационном блоке физико-математических моделей климата (CLIM–5) IPCC рекомендовано использование данных, полученных (Lean et al., 1995) в результате радиометрических измерений общего потока радиации (с 1978 г.) и реконструкции TSI (с 1610 г. с годовым и с 1882 г. с месячным разрешением). (http://solarisheppa.geomar.de/cmip5). Реконструкция общего потока радиации (TSI) выполнена на основе вариаций солнечной активности (чисел пятен и факельных вспышек). Эти реконструированные данные не отражают изменений инсоляционной контрастности, с которыми связан о усиление межширотного теплообмена (работы «тепловой машины первого рода») (Шулейкин, 1953) а также многолетняя изменчивость ПТВ, ТПО и УМО (Федоров, 2016, 2017). Инсоляционная контрастность это разность между годовой радиацией приходящей в область 0 – 45 (источник тепла) и 45 – 90 (стока тепла) в каждом полушарии (для Земли рассчитывается среднее по полушариям). Инсоляционная контрастность отражает изменение в переносе энергии на ВГА.

Учет отмеченного измеренного и реконструированного TSI в качестве входного энергетического сигнала (http://solarisheppa.geomar.de/cmip5) неверен при климатическом моделировании по следующим причинам. Во-первых, он отражает изменение общего прихода радиации к Земле. Это изменение, как показывают выполненные расчеты инсоляции Земли (Bertrand, Van Ypersele, 1999, Berger et al., 2010; Смульский, Кротов, 2013; Федоров, 2015, 2017) незначительно (менее 0.005% за 6000 лет). Эти вариации в приходе солнечной радиации рассчитываются и для отдельных широтных зон по косинусу широты (без учета изменения наклона оси вращения Земли). Однако, поскольку вариации приходящей радиации малы, то и вариации в широтных зонах в этом случае также малы. Важен учет не вариаций в поступлении радиации, а изменчивости в ее распределении по широтным зонам в связи с изменением наклона Земли (эти вариации в годовом распределении за 6000 лет составляют в полярных областях около 2,8%). Рис. 1.

Рис. 1. Широтное изменение годовой инсоляции Земли в интервале
с 3000 г. до н.э. по 2999 г. (Федоров, 2015)

Сходный характер распределения приходящей радиации для отдельных широт получен в работе Смульского и Кротова (2013). Именно этими вариациями определяются тренды в изменении глобальных ПТВ Земли (и ее отдельных широтных зон) (Федоров, 2016, 2017). Применяемый в современных моделях климата учет вариаций приходящей к Земле радиации этого не учитывает (как и не учитывает изменение в переносе энергии на ВГА, http://www.solar-climate.com/sc/psvga.htm). Во-вторых, в моделях не учитывается изменение соотношений вариаций различной физической природы в приходящей радиации (TSI) и их различное влияние на формирование и изменение климата (http://www.solar-climate.com/sc/miztsi.htm).

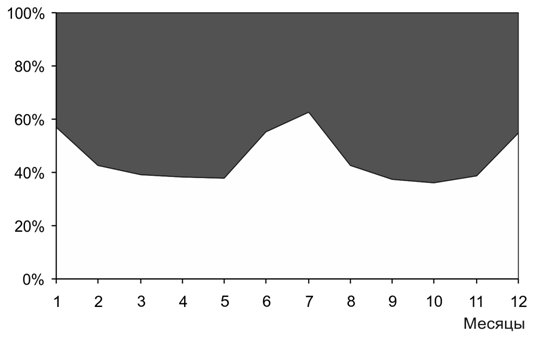
2. Соотношение вариаций разной физической природы в изменчивости TSI. Из рассчитанных данных приходящей радиации (Федоров, 2017) следует, что соотношение вариаций разной физической природы даже в слабо изменяющемся приходе радиации меняется в зависимости от временного разрешения. Например, межгодовая изменчивость инсоляции в диапазоне месячного разрешения на 55% определяется вариациями, связанными с небесно-механическими процессами и на 45% вариациями солнечной активности (рис. 2).

Рис. 2. Соотношение вариаций TSI_SA и TSI_CMP (показаны темным фоном) в межгодовой изменчивости TSI в % в интервале с 1882 по 2008 гг. с месячным разрешением.

Разность значений составляющих межгодовой изменчивости TSI, связанной с небесно-механическими процессами (TSI_CMP) и определяемой изменением активности Солнца (TSI_SA), имеет определенный характер годового хода (рис. 2). Из полученного распределения видно, что при месячном разрешении межгодовые вариации, связанные с активностью Солнца (TSI_SA), превышают веса межгодовых вариаций, определяемых небесно-механическими процессами (TSI_CMP) на протяжении 4 месяцев (1/3 года): июнь, июль, декабрь, январь. Временные интервалы доминирования вариации TSI_SA хронологически локализуются в окрестностях точек летнего и зимнего солнцестояния. На протяжении остальных 8 месяцев (2/3 года) в межгодовой изменчивости TSI преобладает вариация, определяемая небесно-механическими процессами (TSI_CMP). Максимальные значения преобладания вариаций (TSI_CMP) приходятся на интервалы вблизи равноденственных точек. Для периода спутниковых радиометрических наблюдений с 1978 по 2008 гг. среднее соотношение характеризуется весовыми значениями 45,71% (TSI_SA) и 54,29% (TSI_CMP).

Предлагаемые IPCC значения реконструированного TSI не учитывают этого. В связи с полученными результатами рекомендуется в качестве входящего энергетического сигнала при моделировании климата учитывать инсоляцию и/или инсоляционную контрастность связь многолетней изменчивости аномалии ПТВ и ТПО с которой проанализирована и оценена в работах (Федоров, 2016, 2017, http://www.solar-climate.com).

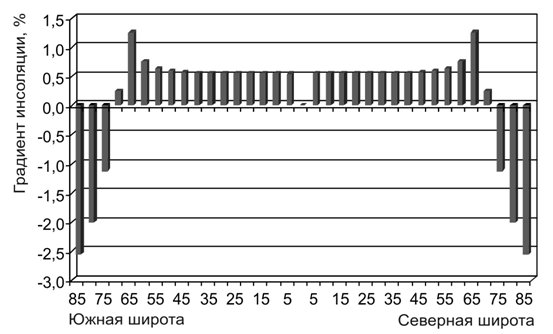
3.Изменение переноса энергии на ВГА. Основными блоками в физико-математических моделях климата являются модели общей циркуляции атмосферы (МОЦА) и модели общей циркуляции океана (МОЦО). Эти блоки описываются системой уравнений гидротермодинамики, отражающей основные физические законы (законы сохранения вещества и энергии, закон сохранения количества движения). Однако, эти уравнения описывают усредненную, статическую атмосферу и океан (Лоренц, 1970; Пальмен, Ньютон, 1973) и не учитывают, например, изменения в переносе лучистой энергии на верхней границе атмосферы. Выполненные расчеты инсоляции (Федоров, 2017) показывают, что в связи с эллипсоидальной формой Земли экваториальная область получает больше лучистой энергии, чем полярные районы. В связи с неравномерностью распределения приходящей радиации на ВГА возникает градиент, которым определяется перенос энергии на ВГА. Отмечается постепенное увеличение переноса лучистой энергии от экватора к полярным кругам в каждом полушарии (рис. 3).

Рис. 3. Изменение годового переноса лучистой энергии по модулю на ВГА за 5998 лет, %.

Физический процесс переноса энергии – излучение. Максимумы увеличения локализованы приблизительно в районе 65-й параллели в каждом полушарии (вблизи полярных кругов). В заполярных областях отмечается постепенное уменьшение (от полярных кругов к полюсам) переноса лучистой энергии. Таким образом, в каждом полушарии выделяются области увеличения (от экватора до полярного круга) и области уменьшения (от полярного круга до полюса) переноса лучистой энергии. Максимальное увеличение (на 2,61Е+15 Вт или 1,25%) отмечается в районе полярных кругов (65° широты) в каждом полушарии («зоны турбулентности»). Максимальное уменьшение переноса (на 3,3Е+15 Вт или 2,56%) приходится на полярные районы (85° широты).

Осредненный перенос энергии в системе океан – атмосфера (Лоренц, 1970; Пальмен, Ньютон, 1973) тесно связан с осредненным переносом энергии на ВГА (Федоров, 2017). Коэффициент корреляции составляет 0,98. Но значения градиента переноса на ВГА на два порядка больше, чем в системе океан – атмосфера (из-за трения в вязкой среде). Поскольку средний годовой перенос энергии в системе океан – атмосфера определяется средним годовым переносом на ВГА, то и полученные для этого переноса изменения на интервале в 5998 лет (от 2999 г. до н.э. до 2999 г. н.э.), могут проявляться и в системе океан – атмосфера. Поскольку перенос энергии отражает межширотный теплообмен (работу тепловой машины первого рода), его в данном случае усиление (Федоров, 2015, 2017). Полученные изменения в переносе энергии на ВГА также следует учитывать в системе уравнений гидротермодинамики (уравнения законов сохранения массы, импульса, энергии и состояния газа) для атмосферы (Гилл, 1986; Педлоски, 1984) используемой при численных экспериментах в физико-математических моделях климата. Используемые в моделях общей циркуляции атмосферы (МОЦА) и океана (МОЦО) уравнения гидротермодинамики описывают статическую атмосферу и океан, которые таковыми в реальности не являются.

Решение этих общих проблем, связанными с успехами в расчетах инсоляции Земли, может способствовать совершенствованию физико-математических моделей климата и прогноза его изменений.

Литература